
Entregas:
- Colisiones I: Introducción, requisitos y alternativas
- Colisiones II: Diseño general de STC
- Colisiones III: Shape y Collision Dispatching
- Colisiones IV: Tests de colisión
En la cuarta entrega de la serie de artículos de documentación sobre el sistema de detección de colisiones de Sion Tower (STC) trataremos en profundidad los tests de colisión. Hasta ahora habíamos visto como funciona la clase abstracta Shape y sus implementaciones así como el Collision Dispatching. Este texto no pretende demostrar la validez de los algoritmos expuestos por la mediana complejidad que algunos entrañan, para una explicación más extensa sugiero acudir a las referencias contenidas en la sección de bibliografía.
Para cada test se ofrece una breve explicación, un diagrama aclaratorio y el algoritmo en C++ utilizando Ogre3D y las clases que hemos visto hasta el momento.
Teorema del plano de separación
El Teorema del eje de separación (separating axis theorem) resulta extremadamente útil en la detección de colisiones. Este teorema asegura que dados dos objetos convexos en un plano 2D existe una línea sobre la cual, las proyecciones de los dos objetos no se solapan si y sólo si los objetos son disjuntos (no tienen puntos en común). Esta línea se conoce como eje de separación. En un espacio tridimensional el eje de separación se convierte en un plano de separación. El siguiente diagrama ilustra el teorema.
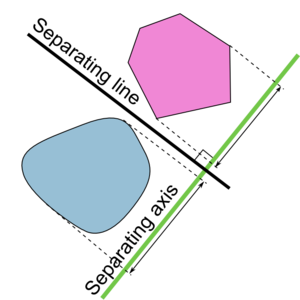
En muchos tests buscaremos el plano de separación, puede que existan varios pero en el momento que encontremos el primero podremos asegurar que los objetos no colisionan (suponiendo que sus formas son convexas). En cualquier videojuego lo normal es que dos objetos cualesquiera no colisionen, por lo que es más eficiente descartar posibles intersecciones cuanto antes. Buscando planos de separación.
Test Sphere-Sphere
El test entre dos esferas es el más sencillo y rápido de todos. Basta con comprobar si la distancia entre los centros de ambas esferas es menor que la suma de sus radios, en tal caso existiría colisión.
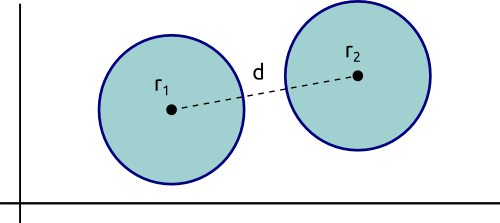
Para calcular la distancia entre dos puntos es necesario una raíz cuadrada pero éstas son extremadamente caras. Podemos comparar la distancia al cuadrado con el cuadrado de la suma de los radios, una expresión equivalente y de mayor eficiencia.
bool Shape::getCollisionSphereSphere(Shape* shapeA, Shape* shapeB) {
// Hacemos la conversión (estamos seguros de que son esferas)
Sphere* sphereA = static_cast<sphere *>(shapeA);
Sphere* sphereB = static_cast</sphere><sphere *>(shapeB);
// Hacemos el test
Ogre::Vector3 s = sphereA->getCenter() - sphereB->getCenter();
Ogre::Real totalRadius = sphereA->getRadius() + sphereB->getRadius();
return (s.squaredLength() < = totalRadius * totalRadius);
}Test AABB-AABB
En la intersección entre cajas alineadas con los ejes emplearemos el teorema del plano de separación. Proyectamos las cajas sobre cada uno de los tres ejes y si algunas de las proyecciones no se solapan podremos asegurar que no existe colisión entre las AABB. El siguiente diagrama ilustra el test.
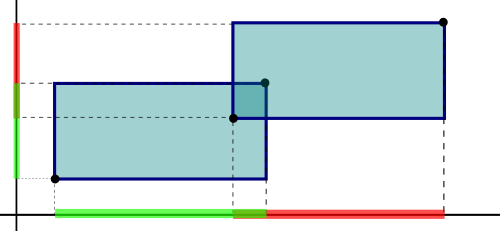
bool Shape::getCollisionAABBAABB(Shape* shapeA, Shape* shapeB) {
// Hacemos la conversión (estamos seguros de que son AABBs)
AxisAlignedBox* aabb1= static_cast<axisalignedbox *>(shapeA);
AxisAlignedBox* aabb2 = static_cast</axisalignedbox><axisalignedbox *>(shapeB);
// Hacemos el test
return (aabb1->getMaxPos().x > aabb2->getMinPos().x &&
aabb1->getMinPos().x < aabb2->getMaxPos().x &&
aabb1->getMaxPos().y > aabb2->getMinPos().y &&
aabb1->getMinPos().y < aabb2->getMaxPos().y &&
aabb1->getMaxPos().z > aabb2->getMinPos().z &&
aabb1->getMinPos().z < aabb2->getMaxPos().z);
}Test Plane-Plane
Los planos son infinitos por lo que la única situación en la que dos planos no colisionan es cuando estos son paralelos y no están a la misma distancia del origen. La orientación de los planos está definida por su vector normal. Si las dos normales son paralelas y la distancia con respecto al origen no coincide podremos asegurar que los planos no colisionan. Dos vectores son paralelos si su producto escalar es igual a 1.
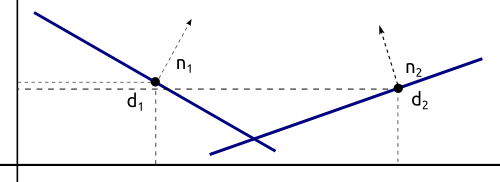
bool Shape::getCollisionPlanePlane(Shape* shapeA, Shape* shapeB) {
// Hacemos la conversión (estamos seguros de que son Planes)
Plane* planeA = static_cast<plane *>(shapeA);
Plane* planeB = static_cast</plane><plane *>(shapeB);
// Hacemos el test
Ogre::Vector3 normalA = planeA->getNormal().normalisedCopy();
Ogre::Vector3 normalB = planeB->getNormal().normalisedCopy();
return normalA.dotProduct(normalB) != 1;
}Test Sphere-AABB
En este test se pueden producir dos casos en los que existe intersección entre los objetos. El primero se da cuando el centro de la esfera está contenida en el AABB mientras que el segundo tiene lugar cuando el centro está fuera de la caja pero existe intersección (el diagrama ilustra el segundo caso). En primer lugar comprobamos si el centro de la esfera está dentro de la caja. Posteriormente recorremos los vértices del AABB y elegimos el más cercano al centro de la esfera. Si la distancia entre ambos es menor que el radio de la esfera las dos formas colisionan.
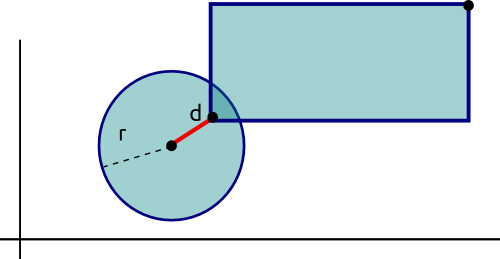
De nuevo, utilizamos el cuadrado de la distancia para conseguir una mayor eficiencia.
bool Shape::getCollisionSphereAABB(Shape* shapeA, Shape* shapeB) {
// Hacemos la conversión (estamos seguros de que A es Sphere y B es AABB)
Sphere* sphere;
AxisAlignedBox* aabb;
if (shapeA->getType() == SPHERE) {
sphere = static_cast<sphere *>(shapeA);
aabb = static_cast<axisalignedbox *>(shapeB);
} else {
sphere = static_cast<sphere *>(shapeB);
aabb = static_cast<axisalignedbox *>(shapeA);
}
// Hacemos el test
Ogre::Real s = 0;
Ogre::Real d = 0;
Ogre::Vector3 center = sphere->getCenter();
Ogre::Vector3 minPos = aabb->getMinPos();
Ogre::Vector3 maxPos = aabb->getMaxPos();
// Comprobamos si el centro de la esfera está dentro del AABB
bool centerInsideAABB = (center.x < = maxPos.x &&
center.x >= minPos.x &&
center.y < = maxPos.y &&
center.y >= minPos.y &&
center.z < = maxPos.z &&
center.z >= minPos.z);
if (centerInsideAABB)
return true;
// Comprobamos si la esfera y el AABB se intersectan
for (int i = 0; i < 3; ++i) {
if (sphere->getCenter()[i] < aabb->getMinPos()[i]) {
s = sphere->getCenter()[i] - aabb->getMinPos()[i];
d += s * s;
} else if (sphere->getCenter()[i] > aabb->getMaxPos()[i]) {
s = sphere->getCenter()[i] - aabb->getMaxPos()[i];
d += s * s;
}
}
return (d < = sphere->getRadius() * sphere->getRadius());
}Test Sphere-Plane
Comprobar si una esfera colisiona con un plano es tan sencillo como obtener la distancia entre ambos y compararla con el radio de la esfera como hemos hecho en otras ocasiones. La distancia entre el centro y el punto que conocemos del plano no es la distancia real entre ambas formas. Para calcular la distancia real tendremos que proyectar el vector p-c (punto del plano – centro de la esfera) sobre la normal del plano.
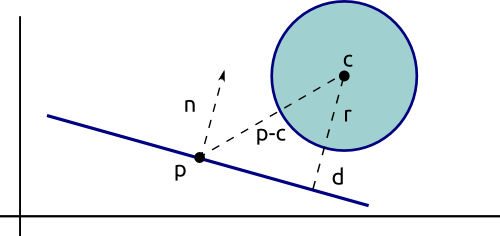
Sólo nos es necesario el cuadrado de la distancia y lo comprobaremos con el cuadrado del radio (para evitarnos utilizar una raíz cuadrada).
bool Shape::getCollisionPlaneSphere(Shape* shapeA, Shape* shapeB) {
// Hacemos la conversión (estamos seguros de que A es Plane y B es Sphere)
Plane* plane;
Sphere* sphere;
if (shapeA->getType() == PLANE) {
plane = static_cast<plane *>(shapeA);
sphere = static_cast<sphere *>(shapeB);
} else {
plane = static_cast<plane *>(shapeB);
sphere = static_cast<sphere *>(shapeA);
}
// Hacemos el test
// Distancia del centro de la esfera al plano
Ogre::Vector3 v = sphere->getCenter() - plane->getPosition();
Ogre::Vector3 n = plane->getNormal().normalisedCopy();
Ogre::Real d = abs(n.dotProduct(v));
// Si d < = radio, hay colisión
return d <= sphere->getRadius();
}Test AABB-Plane
En el test entre AABB y plano calculamos el vértice más lejano y el más cercano al plano (pmin y pmax respectivamente). Si cada punto está a un lado distinto del plano podemos asegurar que ambas formas colisionan.
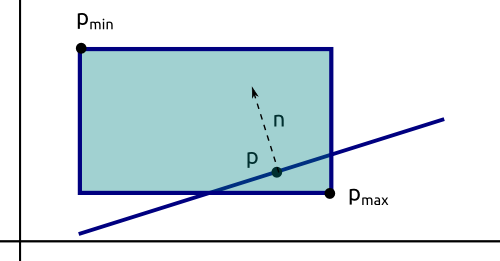
bool Shape::getCollisionPlaneAABB(Shape* shapeA, Shape* shapeB) {
// Hacemos la conversión (estamos seguros de que A es Plane y B es AABB)
Plane* plane;
AxisAlignedBox* aabb;
if (shapeA->getType() == PLANE) {
plane = static_cast<plane *>(shapeA);
aabb = static_cast<axisalignedbox *>(shapeB);
} else {
plane = static_cast<plane *>(shapeB);
aabb = static_cast<axisalignedbox *>(shapeA);
}
// Hacemos el test
Ogre::Vector3 p;
Ogre::Vector3 n;
for (int i = 0; i < 3; ++i) {
if (plane->getNormal()[i] >= 0) {
p[i] = aabb->getMaxPos()[i];
n[i] = aabb->getMinPos()[i];
} else {
p[i] = aabb->getMaxPos()[i];
n[i] = aabb->getMinPos()[i];
}
}
// Si p está en un lado diferente del plano que n, hay intersección
Ogre::Real d1 = plane->getNormal().dotProduct(p - plane->getPosition());
Ogre::Real d2 = plane->getNormal().dotProduct(n - plane->getPosition());
return ((d1 < = 0 && d2 >= 0) || (d1 >= 0 && d2 < = 0));
}Bibliografía
Como podéis comprobar, hay un poco más de fundamento detrás de estos tests de lo que se ha explicado en la secciones anteriores. Para obtener más información sobre este interesante tema, recomiendo las siguientes lecturas (todo en inglés):
- Real Time Collision Detection (Christer Ericson ): excepcional libro que cubre todo lo relacionado sobre la detección de colisiones en 3D escrito por un trabajador de Sony Computer Entertainment America.
- Gamasutra "Simple intersection tests for games" (Miguel Gomez): repaso por varios tests de intersección entre distintos tipos de formas (cubre cuerpos en movimiento).
- Gamasutra "Advanced collision detection techniques" (Nick Bobic): técnicas de detección de colisiones, particionado del espacio y otras optimizaciones.
- Metanet software "Collision detection and response": explicación teórica sobre la detección de colisione. Cuenta con ejemplos gráficos interactivos para ilustrar cada concepto. Me la recomendó el compañero José Tomás Tocino.
En el siguiente artículo lo dedicaremos a las clases Body y CollisionManager del sistema de detección de colisiones de Sion Tower.